24 Février 2016
Mettre la vidéo en pause afin d'essayer et ensuite voir la correction.
Soit  une fonction à valeurs réelles1 définie sur un intervalle
une fonction à valeurs réelles1 définie sur un intervalle  , et
, et  . On dit que
. On dit que  admet un développement limité d'ordre n2 (abrégé par DLn) en
admet un développement limité d'ordre n2 (abrégé par DLn) en  , s'il existe
, s'il existe  réels
réels  et une fonction
et une fonction  tels que
tels que  :
:

 qui tend vers 0 lorsque
qui tend vers 0 lorsque  tend vers
tend vers  , et ce « plus rapidement » que le dernier terme de la somme, c'est-à-dire que :
, et ce « plus rapidement » que le dernier terme de la somme, c'est-à-dire que :
Les fonctions  vérifiant ceci sont notées
vérifiant ceci sont notées  (voir l'article Comparaison asymptotique, et plus précisément la famille des notations de Landau). On écrit donc :
(voir l'article Comparaison asymptotique, et plus précisément la famille des notations de Landau). On écrit donc :

Il est fréquent d'écrire un développement limité en posant 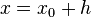 :
:
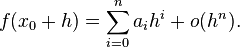
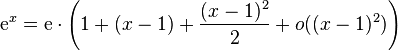
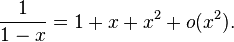

 , alors ce développement est unique et
, alors ce développement est unique et 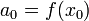 .
. admet un DLn. Ce développement limité se trouve en cherchant un DLn de
admet un DLn. Ce développement limité se trouve en cherchant un DLn de  .
.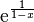
 et en utilisant le DL de eh en 0).
et en utilisant le DL de eh en 0). :
: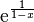 :
:
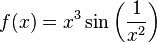 pour tout x non nul et f(0) = 0
pour tout x non nul et f(0) = 0La formule de Taylor-Young assure qu'une fonction f, dérivable n fois au point x0, admet un DLn en ce point :

On le démontre par récurrence sur n, grâce au fait que si la dérivée de f admet un DLn – 1 enx0, alors f admet un DLn en x0, et la partie régulière du DLn – 1 de f' est la dérivée de la partie régulière du DLn de f.
En revanche, le fait qu'une fonction admette un DLn en x0 n'assure pas que la fonction soit nfois dérivable en x0 (par exemple x ↦ x3sin(1/x) – prolongée par continuité en 0 – admet, en 0, un DL2 mais pas de dérivée seconde). On peut juste déduire, de l'existence d'un DL0 enx0, la continuité en x0, et, de l'existence d'un DL1 en x0, la dérivabilité en x0.
soit en écriture abrégée
